数组和链表的区别

虽然网上已经有很多了，但是我还是尝试总结一下，添加一点自己的心得。

总体来说，数组和链表是两种数据结构，所有的异同都是这两种数据结构的特点导致的。这两种数宝结构是计算机的基本数据结构，基态所有都是基于这两种数据结构实现的，只不过在细节上有区别。

简述

数组：多用于读多写少的情况，读取O(1)，写入O(n)，修改O(1)，删除O(n)；需要连续内存。

链表：多用于读少写多的情况，读取O(n)，写入O(1)，修改O(n)，删除O(1)；不需要连续内存。

数据结构差异

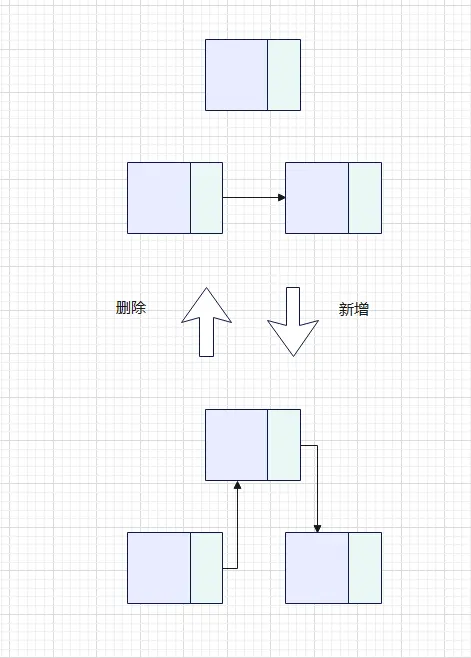
​ 从下图很明显就能看出两者的差别。数组需要连续，即连在一起，而链表不需要，只需要有个指针指向下一个。但是这个指向下一个的指针，也需要占用内存，导致链表中的单个元素比数组中的一个元素的内存大。

增删改查的效率差异

上面的数据结构差异，不可避免的导致了读写性能的差异。

数组

就像把人都聚集在一起，排好大小个顺序放在一个房间(连续内存)里。

查：一般我们查，都是按下标去查数组里的元素，也就相当于知道按大小顺序排的第多少个，直接找到就行。O(1)

改：既然我们能查到某个元素，改的话就是换掉这个元素。就相当于找到某个位置的人，把这个人换掉，一个位置换个人而已。O(1)

增：这时候你需要增加一个人（元素）进来，找到位置，这时候这位置上原本是有人（元素）的，那现在插入的人（元素）来了，这位置和后面位置的人都要向后移一位。   O(n)

删：这刚好和上面的增操作是相反操作。找到合适位置后，踢出这个人（元素），后面位置上的人（元素）都要前进一位。O(n)

链表

就像我们把一个一个人分开，他们每个人只知道排在自己后面的人在什么位置(也可以知道前一个人)，类似于手拉手排队一样。

查：这时候没有具体位置给我们，因为我们也不知道每个人（元素）的具体位置。只是因为大家手拉手（指针）的原因，前一个人能找到排在他后面位置的人。那我们找一个人的时候，就需要每个人都问一边，问一下是不是我们要找的人，不是的话再找下一个，直至找到或者找完。O(n)

改：和上面相同，既然能找到，就能换掉，只不过这次换有点特殊。每个人都是手拉手（指针），我们换掉之后要保证他们还是手拉手（指针）。O(n)

增：这时候你需要增加一个人（元素）进来，找到位置，这时候这位置上原本是有人（元素）的，后面的位置也可能是有人（元素）的，此时我们不要移动后面的人，只需要前后位置人的手牵到的是新增人员（元素）的手行，这样就减少了移动的操作。O(1)

删：这刚好和上面的增操作是相反操作。找到合适位置后，踢出这个人（元素），这位置前后面位置上的人（元素）手拉手就行。O(1)

空间差异

数组

上面也说到了，数组就像把人都聚集在一起，排好大小个顺序放在一个房间(连续内存)里，那对房子的要求就比较高，需要有足够大的房子。如果新增一人，房间（连续内存）不够大了，那所有的人都要换一个大一点的房子进去按顺序排着。这样就不利于扩展，大家都知道大房子（连续内存）是稀缺资源。

链表

而链表就比较友好了，有块空地(内存)就行，因为不需要房子(连续内存)，这样对于空间(内存)利用率就比较高，能把所有没有房子(非连续内存)的地方都用上，这样就比较适合添加人。

扩展

其实计算机的所有底层内存逻辑基本都按这个连续和不连续的模式来的。比如二叉树这种数据结构，说白了也就是链表的一种变种，由链表的指向下一个变成指向下两个。

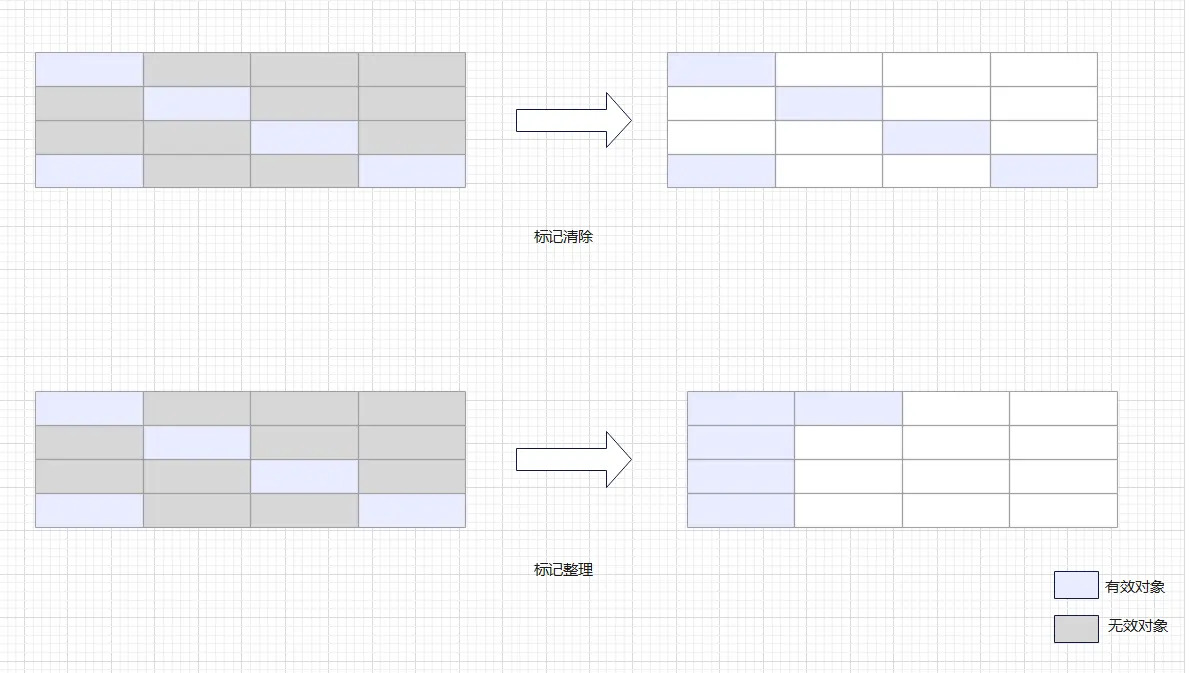
除此之外，在jvm底层的垃圾回收，基本也是按照这种套路，新老代的垃圾回收，各种回收算法。比如标记清理、标记整理。

标记清理: 只是把内存中无效的对象删掉，可以想象，一块内存中，其中有的对象被删了有的没删，这就导致这部分内存可用性就低，因为内存被没删的内存分隔成一小段一小段的，不是连续的。虽然空间利用率不高，但是这种办法简单，只要删掉无效的对象就行。

标记整理: 算法的前部分和标记-清理算法一样，将无效对象删掉，但是资格算法还有后续，将剩余的对象整理一起，放在内存的一端，这样空出的内存就又连续上了。这种算法对空间的利用率就比较好，但是比较麻烦，毕竟要整理嘛。